"Die Akte Astrologie" von Gunter Sachs aus Sicht der Mathematischen Statistik

Herbert Basler

Das Buch "Die Akte Astrologie" sorgte auf dem Buchmarkt für Furore - ein wissenschaftlicher Durchbruch für die Astrologie?

"Noch eine Kritik" mag mancher Leser denken angesichts der Tatsache, daß das 1997 erschienene Buch von Gunter Sachs von den Medien mit hinreichender Aufmerksamkeit bedacht wurde und wohl die meisten bedeutenden (und weniger bedeutenden) Printmedien Rezensionen vorgelegt haben, in denen es an vehementer Kritik der Sachsschen Aussagen keineswegs mangelt. Allerdings werden in den mir zugänglichen Rezensionen immer nur die Sachsschen Interpretationen der jeweiligen statistischen Ergebnisse kritisiert. Ansonsten wird unisono erklärt bzw. unterstellt, daß die statistischen Ergebnisse natürlich stimmen - abgesehen von "kleinen Flüchtigkeitsfehlern", die etwa der Rezensent der Frankfurter Allgemeinen Zeitung bemerkt hat. Eine herausgehoben harsche Kritik - die man wohl den Versuch eines Verrisses nennen muß - liefert Dr. Peter Niehenke in Esotera 1/98, der gemäß Einleitungstext "einer der führenden Astrologen Deutschlands" ist und unter anderem auch "Mathematik studiert" hat. Aber auch Niehenke übt gegenüber den mathematisch-statistischen Ergebnissen von Sachs und seinen Beratern den üblichen, bequemen Autoritätsgehorsam, indem er am Schluß seiner Kritik schreibt: "Die statistische Auswertung bei dieser Untersuchung ist sicher fehlerfrei, daran habe ich nicht den geringsten Zweifel." Eine spezielle Variante von Autoritätsgehorsam bietet der Rezensent der Süddeutschen Zeitung. Er teilt nämlich mit, daß "ein Statistik-Professor an der Universität München bescheinigt, die Studie sei statistisch korrekt".

Sämtliche Boulevardbläter berichteten in höchsten Tönen über Gunter Sachs und seinen "Beweis für die Astrologie".

Dazu wird in der vorliegenden Kritik einiges nachgeholt. Denn die Herleitung der im Buch von Sachs vorgelegten statistischen Ergebnisse enthält durchgängige handwerklich-methodische Fehler. Beispielsweise wird nachfolgend für den Zusammenhang zwischen Sternzeichen(1) und Suizid - den Kritiker Niehenke ausführlich begutachtet - gezeigt: Die von Sachs für fünf von den zwölf Sternzeichen gemachte Aussage, daß die jeweilige tatsächliche Suizidanzahl statistisch signifikant von der betreffenden "Zufallserwartung" abweicht, erweist sich beim Nachrechnen für vier dieser fünf Sternzeichen als falsch - jedenfalls sind diese vier Abweichungen auf dem von Sachs jeweils angegebenen Signifikanzniveau nicht signifikant(2).

Die Allensbacher Sternzeichen-Studie - Vergleiche von Unvergleichbarem

Im zweiten Teil des Buches von Sachs wird eine umfangreiche Studie des Allensbacher Instituts für Demoskopie veröffentlicht (ca. 120 Seiten) zu der Frage nach eventuellen Zusammenhängen zwischen den Antworten von befragten Personen auf demoskopische Fragen und den Sternzeichen, unter denen die befragten Personen geboren wurden. Insgesamt wurden Antworten von 13 283 Personen auf 923 Fragen ausgewertet, wobei allerdings das jeweilige Tierkreiszeichen nur bei 10 758 dieser Personen ermittelt werden konnte, weil die übrigen 2525 Personen die Frage nach ihrem Geburtstag nicht beantwortet hatten. Aufgegliedert nach den zwölf Tierkreiszeichen werden die Befragungsergebnisse auf 51 Tabellenseiten (S. 280-332) wiedergegeben(3). Grafisch dargestellt werden jene 30 Merkmale, bei denen sich bei einzelnen Tierkreiszeichen "signifikante Abweichungen vom Mittelwert aller Befragten ergeben". In der aus dem Sachs-Buch übernommenen Abb. 1 (S. 233, dort "Graphik 2") sind beispielsweise die "Abweichungen vom Mittelwert beim besonderen Interesse für das Bauen, Modernisieren und Renovieren" angegeben, woraus man abliest: 17,6 % der Befragten zeigten "besonderes Interesse", im folgenden kurz als 17,6 % Ja-Antworten bezeichnet. Beim Sternzeichen Fische wurden hingegen 22,1 % Ja-Antworten ermittelt, die grafisch dargestellte Abweichung beträgt also 22,1 % - 17,6 % = + 4,5 % . Betrachtet man in Abb. 1 alle zwölf Abweichungen vom Mittelwert, so fällt sofort auf, daß merkwürdigerweise die positiven bweichungen augenfällig überwiegen, während doch auch jeder Laie vermuten wird, daß die Summe aller positiven und negativen Abweichungen eigentlich Null sein sollte, d. h. man vermutet, daß die angegebenen positiven Abweichungen fehlerhaft überhöht sind. Einer weiteren Tabelle im Sachs-Buch (S. 290) entnimmt man, daß die Abweichung für Zwillinge mit +3,4 % hochsignifikant ist (Signifikanzniveau 1 % ), d. h. daß Zwillinge "überzufällig häufig" mit Ja antworten - und damit erst recht Fische mit der noch größeren Abweichung von +4,5 % . Allensbach gibt also an, daß ein hochsignifikanter Zusammenhang zwischen den genannten Sternzeichen der Befragten und deren Antwortverhalten bestehe. Aufgrund der bereits ausgesprochenen Vermutung der fehlerhaft überhöhten Abweichungen kann man jetzt naturgemäß weiter vermuten, daß auch die beiden Signifikanzaussagen eventuell gar nicht zutreffen. Dies ist tatsächlich so. Denn der angegebene "Mittelwert" von 17,6 % ist der Anteil der Ja-Antworten unter allen 13 283 Befragten und nicht der für den angestrebten Vergleich der zwölf Tierkreiszeichen untereinander ausschließlich geeignete Anteil der Ja-Antworten unter den nur 10 758 Personen, deren Tierkreiszeichen ermittelt werden konnte. Rechnet man aus den zwölf angegebenen Anzahlen von Befragten (z. B. 837 für Steinböcke) und den zugehörigen Prozentangaben der Ja-Antworten (z. B. 18,2 % für Steinböcke) die jeweilige Anzahl von Ja-Antworten aus (z. B. 152 für Steinböcke), so erhält man insgesamt 2038 Ja-Antworten für die 10758 "Personen mit bekanntem Tierkreiszeichen", also einen Anteil von 18,9 % Ja-Antworten anstatt des von Allensbach unzulässigerweise für den angestrebten Vergleich der zwölf Tierkreiszeichen herangezogenen Anteils von 17,6 %, der von Allensbach als "Mittelwert" bezeichnet wird. Hätte Allensbach die Ja-Anteile 22,1 % für Fische und 21,0 % für Zwillinge mit dem Ja-Anteil von 18,9 % verglichen, so hätten sich die Abweichungen in beiden Fällen nicht als hochsignifikant herausgestellt. (Das einschlägige professionelle Testverfahren ist jeweils ein Chi-Quadrat-Test in einer 4-Felder-Tafel, der in beiden Fällen keine Signifikanz auf einem Signifikanzniveau von 1 % ergibt.)

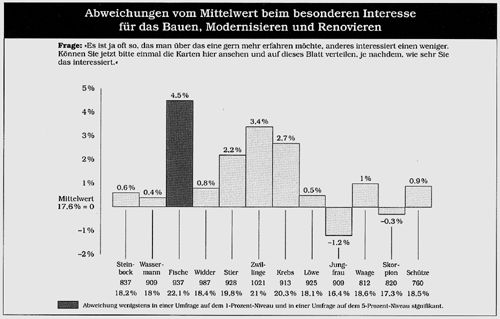
Abb. 1: Im Buch von Gunter Sachs findet sich auf Seite 233 im Anhang diese bemerkenswerte Grafik.

Dieser durchgängige Fehler stellt prinzipiell sämtliche in der Allensbach-Studie aufgeführten Auswertungen und ausgewiesenen Signifikanzen in Frage, z. B. auch die nach Sternzeichen aufgegliederten Interessen für Politik, Umweltschutz usw. Jeder Leser wird sich natürlich fragen, wie solch ein gravierender Fehler unterlaufen kann, daß man Unvergleichbares vergleicht oder auch, ob nicht vielleicht der Rezensent falsch urteilt. Eine Erklärung liegt vielleicht darin, daß dieser Fehler numerisch dann nicht ins Gewicht fällt, wenn sich das Antwortverhalten der 10 758 "Befragten mit Tierkreiszeichen" und der 2525 "Befragten ohne ermitteltes Tierkreiszeichen" nicht unterscheidet. Dies trifft jedoch im vorliegenden Fall keinesfalls zu. Denn berechnet man aus dem angegebenen Ja-Anteil von 17,6 % aller Befragten die Anzahl der Ja-Antworten zu 2338 (wofür die nicht hinreichend genaue Angabe von 17,6 % als 17,60 % gedeutet wird), so erhält man 2338 - 2038 = 300 Ja-Antworten für die 2525 "Befragten ohne Tierkreiszeichen" - also 11,9 %, während der Ja-Anteil der "Befragten mit Tierkreiszeichen" 18,9 % betrug! Diese beiden Ja-Anteile unterscheiden sich höchst signifikant. (Für die Testgröße des einschlägigen Chi-Quadrat-Tests ergibt sich der Wert 70,3 bei einer Testschranke von 10,83 zum Signifikanzniveau a=0,001 ). Dies bedeutet also, daß die Zielfrage nach dem "Bauen" usw. von den Personen, die nicht bereit waren, ihr Geburtsdatum anzugeben (= partielle Antwort-Verweigerer), wesentlich anders beantwortet wurde wie von den übrigen Befragten.

Dieser Effekt, daß das Antwortverhalten bezüglich der Zielfrage vom Antwortverhalten bezüglich der Nebenfrage (z. B. nach dem Geburtstag) abhängt, ist für die Demoskopie u. a. deshalb so unangenehm, weil die Stärke dieses Effekts bei den unterschiedlichen 923 Zielfragen unterschiedlich groß ist, so daß keine einheitliche Korrektur dieses Effekts möglich ist. Von hier aus erscheint das in der Demoskopie bekannte Problem, ob und wie Antwort-Verweigerer das Gesamtergebnis zu einer Frage beeinflussen, in besonders grellem Licht. Auf methodische Einwände im Sinne der Mathematischen Statistik (Durchführung sehr vieler Einzeltests anhand des gleichen Materials, was im Buch von Sachs verschiedentlich als "multiples Testproblem" angesprochen wird; fehlender Globalvergleich aller zwölf Tierkreiszeichen untereinander, den Sachs im ersten Teil des Buches sogar selbst verlangt, S. 48) soll hier zunächst verzichtet werden, da das Allensbacher Institut die vorgelegte Untersuchung selbst lediglich als eine "Pilot-Studie" bezeichnet, und in dieser Bezeichnung wohl die prophylaktische Bitte um Vergebung einiger statistischer Sünden zum Ausdruck kommt.

Sternzeichen und Suizid

In dem Kapitel "Wer wählt den Freitod?" präsentiert Sachs das auszuwertende Datenmaterial folgendermaßen: "Es standen uns die Geburtsdaten von 30 358 Frauen und Männern zur Verfügung, die in den Jahren 1969 bis 1994 in der Schweiz den Freitod gewählt haben. Die Mitarbeiter der Sektion Gesundheit des Statistischen Bundesamtes in Bern lieferten uns als Grundlage die nachstehende Tabelle" (hier wiedergegeben als Tab. 1).

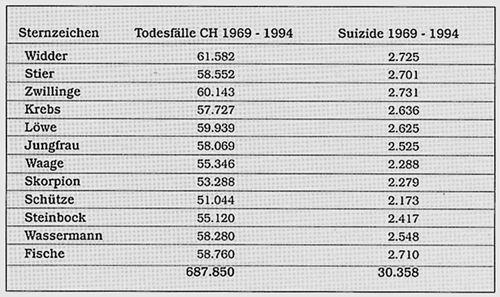
Tab. 1: Aus dem Buch von Gunter Sachs (S. 159) übernommene Tabelle zu Sternzeichen und Selbstmorden.

Dieser scheinbar so klare Einführungstext bedarf einiger Ergänzungen, die die statistische Auswertung wesentlich betreffen. Im vorangehenden Kapitel "Wer stirbt woran?" erfährt man (S.149f): "Als Ausgangsmaterial standen uns die Daten aller in der Schweiz in den Jahren 1969 bis 1994 verstorbenen Frauen und Männer zur Verfügung, aufgeteilt nach deren Sternzeichen sowie untergliedert nach 32 verschiedenen Todesursachen. Insgesamt handelte es sich dabei um 1 195 174 Todesfälle. In Abstimmung mit den uns beratenden Statistikern wurde diese Datenmenge für unsere Untersuchung weiter aufbereitet." Diese "Aufbereitung" besteht im Fortlassen von Todesursachen "mit zu geringem zahlenmäßigen Umfang" und solchen, "die vom Standpunkt der Astromedizin keinen oder nur geringen Aussagewert besitzen". Damit wurde "das für die Auswertung maßgebende Datenmaterial auf 20 Todesursachen bei 687 850 Verstorbenen reduziert", also um mehr als 40 %. Da unter den 20 verbliebenen Todesursachen Suizid nicht aufgeführt ist, heißt das, daß mit der Tabellenüberschrift Todesfälle CH 1969-1994" die Teilmenge derjenigen Todesfälle mit 20 bestimmten Todesursachen gemeint ist, in der also die vom Statistischen Bundesamt in Bern angegebenen Suizide nicht enthalten sind.

Dies bedeutet für den Statistiker: Die Frage nach einem Zusammenhang zwischen Sternzeichen und Suizid ist aufgrund dieses Datenmaterials mit Hilfe des Chi-Quadrat-Tests auf Unabhängigkeit der 12-klassigen Sternzeichen-Einteilung und der 2-klassigen Todesursachen-Einteilung (Suizid oder eine der 20 Todesursachen) in einer 12 x 2-Felder-Tafel zu testen. Diese Formulierung der Aufgabenstellung ist äquivalent mit der wohl anschaulicheren Frage, ob sich die zwölf empirischen Suizidanteile (z. B. 2725 von 30.358 = 8,98 % für Widder) und die zugehörigen zwölf empirischen 20-Ursachen-Todesfälle-Anteile (z. B. 61 582 von 68 7850 = 8,95 % für Widder) signifikant unterscheiden. Damit ist sofort klar, daß Sachs einen Modellierungsfehler begeht bzw. das falsche Testverfahren wählt, da er nämlich denjenigen Chi-Quadrat-Test benutzt, der die zwölf empirischen Suizidanteile mit zwölf numerisch fest vorgegebenen, nicht zufallsabhängigen Anteilswerten zu vergleichen gestattet, nämlich den sogenannten Chi-Quadrat-Anpassungstest. Sachs wertet also so aus, als ob z. B. sein Widder-Anteil von 8,95 % der Widder-Anteil unter den Todesfällen schlechthin wäre - was allein aufgrund der Herkunft dieses Wertes keineswegs der Fall
ist. Obwohl die Anteile der verschiedenen Sternzeichen an "den Todesfällen" bzw. "den Geburten" keine Konstanten sind, - was noch gezeigt werden wird - sind beispielsweise die jährlichen Schwankungen dieser Parameter bei größeren Populationen von Population zu Population relativ klein, so daß im vorliegenden Fall bei dem Populationsumfang von 687 850 Todesfällen die Unterschiede zwischen den Ergebnissen des inadäquaten Anpassungstests und des Unabhängigkeitstests numerisch nicht allzu groß ausfallen. Dennoch sind, wie noch gezeigt werden wird, solche kleinen Schwankungen dieser Parameter geeignet, viele ansonsten auffällige Signifikanzen zu erklären. Bemerkenswert erscheint noch, daß Sachs im Kapitel "Wer stirbt woran?" den Zusammenhang zwischen den Sternzeichen und den einzelnen 20 Todesursachen insoweit korrekt behandelt, als er dort den Chi-Quadrat-Unabhängigkeitstest verwendet.

Testergebnisse: Sachs gibt als Ergebnis der Anwendung des (inadäquaten) Anpassungstests an, daß bei einer zu akzeptierenden Irrtumswahrscheinlichkeit von 0,00084 die empirische Aufteilung der Suizide auf die zwölf Sternzeichen von der Verteilung der Todesfälle abweicht. Dieser Wert ist korrekt. Er gehört zu dem Wert 31,7 der Testgröße des Anpassungstests. (Leider gibt Sachs bei keinem der durchgeführten Tests den Wert der Testgröße an, was Überprüfungen beträchtlich erschwert.) Demgegenüber erhält man für die Testgröße des korrekten Unabhängigkeitstests den Wert 30,4 bei Testschranken von 31,3 zum Signifikanzniveau a = 0,001 und 24,7 zu a = 0,01. Das heißt, die Unabhängigkeitshypothese kann zwar nicht mehr wie aufgrund des Sachsschen Ergebnisses bei a = 0,001 abgelehnt werden aber immerhin noch bei a = 0,01. Anders formuliert: Bei Zugrundelegung einer Sicherheitswahrscheinlichkeit von 99 % ist statistisch nachgewiesen, daß zwischen Sternzeichen und Suiziden ein statistischer Zusammenhang besteht - ein erstaunliches Resultat aus der Sicht von Astro-Skeptikern - zunächst jedenfalls. Sachs testet sodann für jedes der zwölf Sternzeichen einzeln, ob der jeweilige Suizidanteil signifikant vom betreffenden Anteil der Todesfälle abweicht - naturgemäß wohl wieder mit dem inadäquaten Anpassungstest - und gibt die folgenden fünf signifikanten Ergebnisse an (Tabelle auf S. 162):

• Signifikante Abweichung bei a = 0,05 für Stier, Krebs und Schütze.
• Signifikante Abweichung bei a = 0,01 für Fische.
• Signifikante Abweichung bei a = 0,001 für Waage.

Führt man den korrekten Unabhängigkeitstest (als Chi-Quadrat-Test in der jeweiligen 2 x 2-Felder-Tafel) für diese fünf Sternzeichen durch, so erhält man für die Testgröße (in der vorangehenden Reihenfolge Stier, Krebs, ,Waage) die Werte 5,52; 3,19; 2,93; 5,49 und 10,23. Die Werte der Testschranke sind 3,84 für a = 0,05; 6,63 für a = 0,01 und 10,83 für a = 0,001. Vergleicht man diese fünf Testergebnisse mit den Angaben von Sachs, so sieht man: Nur für das Sternzeichen Stier kann die Unabhängigkeitshypothese auf dem von Sachs angegebenen Signifikanzniveau abgelehnt werden. Die übrigen vier Signifikanzaussagen von Sachs sind falsch - jedenfalls hinsichtlich des angegebenen Signifikanzniveaus. Allerdings bleibt festzustellen: Für die Sternzeichen Stier und Fische ist ein statistischer Zusammenhang mit Suizid bei Zugrundelegung einer Sicherheitswahrscheinlichkeit von 95 % nachgewiesen und für das Sternzeichen Waage sogar bei Zugrundelegung einer Sicherheitswahrscheinlichkeit von 99 % - ein immerhin erstaunliches Resultat aus der Sicht von Astro-Skeptikern - zunächst jedenfalls.

Wie kann man die gravierenden Abweichungen zwischen den Sachsschen Signifikanzangaben und den korrekten Testergebnissen erklären? Sachs unterscheidet in seiner Darstellung bei Tests, die einzelne Sternzeichen betreffen, zwischen positiven und negativen Abweichungen von der jeweiligen "Zufallserwartung", d. h. er glaubt vermutlich, den Test jeweils einseitig anwenden zu dürfen und lehnt z. B. bei einem vorgegebenen a = 0,05 die Nullhypothese sowohl dann ab, wenn die empirische Abweichung in eine 5 %ige Ablehnregion im Negativen fällt als auch dann, wenn diese Abweichung in die entsprechende Ablehnregion im Positiven fällt. Dies bedeutet, daß er die vorgegebene Irrtumswahrscheinlichkeit von 5 % nicht einhält, sondern eine tatsächliche Irrtumswahrscheinlichkeit von 10 % benutzt! Allein dieser Fehler kann die festgestellten Differenzen zwischen den fünf Signifikanzangaben von Sachs und den korrekten Testergebnissen erklären.

Die einseitige Durchführung dieser Tests wäre nur dann zulässig gewesen, wenn bereits vor Einsichtnahme in das Stichprobenmaterial für jedes der zwölf Sternzeichen festgestanden hätte bzw. festgelegt worden wäre, für welche der beiden möglichen Abweichungsrichtungen man die Nullhypothese bei Überschreiten der betreffenden Testschranke abzulehnen gedenkt. Eine solche Situation kann bei Untersuchungen durchaus gegeben sein; typischerweise dann, wenn aufgrund früherer Untersuchungen oder z. B. astrologisch-theoretischer Überlegungen nur noch die Frage zu testen ist, ob Unabhängigkeit vorliegt oder signifikant positive Abweichungen, während eventuelle negative Abweichungen nicht mehr von Interesse sind. Die Frage, ob solche begründeten Festlegungen einer einseitigen Fragestellung bereits vor Einsichtnahme in die Daten erfolgt sind oder nicht, kann gelegentlich zu Diskussionen führen - zwischen Puristen als Vertretern einer reinen Lehre und Praktikern im Sinne der real-existierenden Statistik. Im vorliegenden Fall liegen jedoch glückliche Verhältnisse vor, denn zum einen trifft Sachs keinerlei solche Voraus-Festlegungen. Zum anderen belegt Sachs seine Unvoreingenommenheit mit dem Hinweis darauf, daß sich seine Ergebnisse "nicht in allen Fällen mit dem Bild in der (astrologischen) Literatur decken" (S. 161), d. h. er betont geradezu, daß er bei jedem einzelnen Test für die zwei Seiten (positive und negative Abweichungen) offen war und also zweiseitig hätte testen müssen. Hinzu kommt, daß der bereits zitierte Astrologe Niehenke bestreitet, daß Astrologie Aussagen über Zusammenhänge zwischen Tierkreiszeichen und Suizid machen könne.

Diesen "Einseitigkeits"-Fehler begeht Sachs durchgängig, u. a. auch, wenn er im Kapitel "Wer heiratet wen?" jede einzelne der 12 x 12 = 144 möglichen Sternzeichenkombinationen der Partner bei Eheschließungen daraufhin untersucht, ob die jeweilige tatsächliche Anzahl einer Kombination von der bei Unabhängigkeit zu erwartenden Anzahl signifikant abweicht. Da dann etwa bei seiner Vorgabe des Signifikanzniveaus zu a = 0,05 die faktisch benutzte Irrtumswahrscheinlichkeit 10 % beträgt, so sind auch unter der Annahme des Zutreffens der Unabhängigkeitshypothese 10 % Scheinsignifikanzen, also durchschnittlich 14,4 Scheinsignifikanzen (= reine Zufallssignifikanzen = Fehlsignifikanzen) zu erwarten, und es ist mit den Methoden der Mathematischen Statistik nicht mehr entscheidbar, welche seiner 25 gefundenen Signifikanzen (S. 74f) lediglich Scheinsignifikanzen darstellen. Dieses durchgängig relevante methodische Problem wird - abgesehen von dem "Einseitigkeits"-Problem - im Buch von Sachs zwar angesprochen und als "multiples Testproblem" bezeichnet (z. B. S. 208) - aber angemessene Konsequenzen werden nicht gezogen. (Die Diplomstatistikerin und Sachs-Beraterin Dr. Künstler schreibt zwar (S. 208), daß "die Möglichkeit eines ,multiplen Testproblems' gegeben war", man sich aber nur bei der Untersuchung über "Krankheiten und Berufe" dazu "entschlossen" habe, "leichte Signifikanzen nicht auszuweisen", sondern "lediglich als Hinweise zu bezeichnen", weil bei dieser Untersuchung die Anzahl der Einzeltests "besonders groß ist" - sie beträgt 12 x 47 = 564. Aber auch zu dieser Vorsichtsmaßnahme habe man sich "entschlossen", obwohl sie nach Ansicht der Berater nicht zwingend erforderlich gewesen wäre.)

Methodisch einwandfreies Vorgehen erfordert folgende Konsequenzen: Aufgrund eines für eine Erstuntersuchung vorgelegten Datenmaterials darf nur das Ergebnis des betreffenden globalen Unabhängigkeitstests gegebenenfalls als ein statistisch signifikanter Zusammenhang angegeben werden. Abweichungen bei den z. B. 144 Einzeltests dürfen gegebenenfalls (d. h. bei Überschreiten der Testschranke) lediglich als Vermutungen oder Hinweise ausgewiesen werden. Sie können und sollten auf der Basis neuen Datenmaterials getestet werden, wobei es zulässig ist, jetzt vor Einsichtnahme in das Datenmaterial festlegbare einseitige Fragestellungen zu testen. Erst danach sind methodisch einwandfreie Signifikanzaussagen zu Einzel-Zusammenhängen möglich, z. B. zu der Frage, ob bei Ehepaaren tatsächlich ein so hochsignifikanter negativer Zusammenhang zwischen Wassermann-Männern und Stier-Frauen besteht, wie von Sachs methodisch gesehen vorschnell ausgewiesen (S. 74). Offensichtlich müssen aus dieser Situation Erwartungen an Herrn Sachs erwachsen hinsichtlich einer "Akte II" - eine wohl nicht ganz unziemliche Erwartung, da doch die bisherigen Kosten der Studie ("unter dem Fabrikpreis eines Porsche 911, Baujahr 1997", S. 210) vermutlich unversehens als Bestseller-Honorare zurückgeflossen sind - eventuell mit Zinsen.

Die vorangehenden Ausführungen zum "multiplen Testproblem" betreffen natürlich auch die Allensbach-Studie im Sachs-Buch gravierend, da allein bei der Auswertung der beiden zusammengefaßten Stichproben für die 923 Fragen 923 x 12 Einzeltests durchzuführen waren.

Signifikanz - ein Zauberwort?

Wenn in einem Buch so unüberschaubar viele Signifikanzen ausgewiesen werden wie im Buch von Sachs, so ist es sicherlich wichtig, daß man die grundsätzliche Bedeutung eines statistisch signifikanten Ergebnisses nicht verkennt und vor allem nicht überbewertet. Davor scheint Sachs allerdings selbst nicht gefeit zu sein, denn er erklärt den Lesern die Bedeutung eines signifikanten Ergebnisses anhand "eines bewußt vereinfachten Beispiels" folgendermaßen (S. 78):

"Nehmen wir an, 100 Personen sind von einer unbekannten Krankheit befallen. Alle 100 erhalten ein neues Medikament. Nun werden 75 Patienten geheilt. Der Fall wäre nach unseren Kriterien nicht signifikant, die Heilkraft des Medikaments statistisch nicht nachgewiesen. Bei der Heilung von 95 der hundert Kranken würden wir die Wirkung als ,leicht signifikant' bezeichnen. Erst bei 99 Genesungen würden wir die Heilkraft als ,signifikant' bewerten."

Zunächst wird wohl auch jeder Laie sofort einwenden, daß hier etwas nicht stimmen kann. Denn wäre die "unbekannte Krankheit" eine unheilbare Krankheit, wie etwa AIDS, so wären doch wohl die Entdecker eines "neuen Medikaments", das bei seiner Erprobung an 100 Patienten zu 75 Heilungen geführt hat, offenkundig unschlagbare Kandidaten für Nobelpreise - und das Nobelkomitee würde wohl gar nicht erst Statistiker für einen Wirksamkeitsnachweis bemühen. Aber selbst wenn man das Beispiel dahingehend präzisiert, daß man die Wahrscheinlichkeit für eine Spontanheilung (also ohne Medikament) beispielsweise zu 50 % annimmt, so daß also der Wirksamkeitsnachweis für das Medikament in dem statistischen Nachweis besteht, daß die Heilungswahrscheinlichkeit mit Medikament größer als 50 % ist, selbst dann wäre aufgrund des Stichprobenergebnisses "75 Heilungen bei 100 Patienten" der Wirksamkeitsnachweis erbracht und zwar in höchst signifikanter Form. (Für die Testgröße des Chi-Quadrat-Anpassungstests erhält man den Wert 25,0 bei der Testschranke 10,83 für a = 0,001 - wobei hier sogar die kleinere einseitige Schranke angemessen wäre.)

Ergänzend sei angefügt: Für den vorangehend präzisierten Wirksamkeitsnachweis reichen auf den drei üblichen Signifikanzniveaus die folgenden Mindestanzahlen von Heilungen (bei 100 Patienten) aus: 59 Heilungen bei einem Signifikanzniveau von 5 % (a = 0,05), 63 Heilungen bei einem Signifikanzniveau von 1 % (a = 0,01), 66 Heilungen bei einem Signifikanzniveau von 1 % o (a = 0,001).

Dies bedeutet, daß das von Sachs gewählte Demonstrationsbeispiel eine hoffnungslos überhöhte Aussagekraft eines statistisch signifikanten Ergebnisses vortäuscht. Hiernach ist wohl die Möglichkeit nicht ganz auszuschließen, daß das in diesem Beispiel zum Ausdruck kommende bizarre Mißverständnis von "Signifikanz" auch ursächlich ist für die oft etwas ungezügelten Sachs'schen astrologischen Interpretationen seiner signifikanten statistischen Ergebnisse.

Gibt es unsterbliche Fische? - Oder: Was ist eine Stichprobe?

Bei der Anwendung jedes statistischen Testverfahrens muß unterstellt werden, daß das auszuwertende Datenmaterial das Ergebnis einer Zufallsstichprobe im Sinne der Mathematischen Statistik darstellt. Gegen diese auch bei den vorliegenden statistischen Untersuchungen stets stillschweigend unterstellte Modellannahme werden nachfolgend gravierende Einwände erhoben und belegt.

Zur Demonstration dieses Problems soll zunächst folgende Nullhypothese getestet werden: Die Aufteilung "der Todesfälle" auf die zwölf Sternzeichen ist identisch mit der Aufteilung "der Geburten" auf die zwölf Sternzeichen.

Als Datenmaterial sollen folgende Angaben aus dem Buch von Sachs verwendet werden: Die Aufteilung der 2 731 766 "Geburtenzahlen der Volkszählung Schweiz 1990, Jahrgang 1925-1960" (S. 114 und S. 116) als hypothetische Verteilung und als Stichprobe die vorstehend bereits verwendete Aufteilung der 687 850 "Todesfälle CH 1969-1994". Als Testergebnis erhält man (mit dem Chi-Quadrat-Anpassungstest) eine exorbitant signifikante Abweichung, z. B. beträgt der Fische-Anteil an den Geburtenzahlen 240 677 von 2 731 776, also 8,81 % während der Fische-Anteil an den Todesfällen gemäß obiger Tabelle nur 8,54 % beträgt - eine höchst signifikante Abweichung. (Die Testgröße des Chi-Quadrat-Anpassungstests ergibt den exorbitanten Wert 61,4.)

Dieses Testergebnis erweckt offensichtlich den Anschein, als ob damit die Existenz unsterblicher Fische statistisch höchst signifikant nachgewiesen wäre. Als typische Reaktion von Kritikern muß man wohl vermuten: "Statistisch natürlich korrekt, aber aufgrund praktischer Erfahrung irrelevant" - worin einmal mehr die verbreitete Ansicht zum Ausdruck käme, gemäß der die Statistik lediglich eine Veranstaltung für tumbe Rechenknechte und Zahlenfriedhofsgärtner ist.

Die eindeutige Folgerung aus diesem Nonsens-Beispiel - nämlich eine Hypothese zu testen, die wegen der allgemein anerkannten Sterblichkeit aller Menschen unbezweifelbar zutrifft - lautet: Jedenfalls stellt die Menge der "Todesfälle CH 1969-1994" keine Zufallsstichprobe aus einer Geburten-Population dar, die bezüglich der Sternzeichen so verteilt ist, wie die benutzte Geburten-Population "Geburtenzahlen CH 1925-1960".

Nun zu der Frage, was dieses Nonsens-Beispiel mit den von Sachs durchgeführten Vergleichen zu tun hat, etwa mit dem hier bereits behandelten Vergleich der "Suizide CH 1969-1994" mit den "Todesfällen CH 1969-1994"? Offensichtlich läßt sich für beide Vergleiche feststellen, daß die jeweils herangezogenen beiden Populationen hinsichtlich der Geburtsjahrgänge nicht vollständig übereinstimmen: Im Nonsens-Beispiel ist offensichtlich, daß die Todesfälle bezüglich der Geburtsjahrgänge nicht repräsentativ für die benutzte Vergleichspopulation von Geburten sind, aber auch beim Sachsschen Vergleich stimmen Alter bzw. Jahrgang der Suizidfälle und der übrigen Todesfälle vermutlich nicht überein - mindestens macht er dazu keinerlei empirische Angaben. Allerdings würden solche unterschiedlichen Geburtsjahrgänge den jeweiligen Vergleich dann nicht beeinträchtigen, wenn die Sternzeichenverteilung über die Jahrgänge hinweg stabil bliebe. Dieses Problem wird von Sachs durchaus gesehen und angesprochen (S. 107): " denn die Verteilung der Geburtenhäufigkeiten im Jahresablauf ist aberJahrzehnte hinweg nahezu unverändert so daß wir für praktische Zwecke von einer relativen Konstanz der Geburtenverteilung im Jahresverlauf ausgehen dürfen."

Hier muß hinzugefügt werden: Vergleicht man die Sternzeichenverteilung für die vorangehend benutzten "Geburtenzahlen CH 1925-1960" mit den von Sachs an anderer Stelle (S. 108 und S. 110) verwendeten "Geburtenzahlen CH 1954-1976", so erweisen sich diese beiden Verteilungen als höchst signifikant verschieden; z. B. beträgt der Fische-Anteil für 1954-1976 nur 8,48 % gegenüber dem bereits verwendeten Fische-Anteil von 8,81 % von 1925-1960. (Die Testgröße des Chi-Quadrat-Tests für den Fische-Vergleich besitzt den exorbitanten Wert 179,9, d. h. die aufgrund fehlender Daten nicht eliminierbare Überlappung der beiden Geburten-Populationen fällt für die Signifikanzfrage nicht ins Gewicht.) Dies bedeutet, daß man Sachs zwar zustimmen kann, wenn er meint, daß man für "praktische Zwecke von einer relativen Konstanz" ausgehen darf, aber eben nicht für die Zwecke seiner statistischen Untersuchungen, die stets auf so großen Stichprobenumfängen basieren, daß auch winzige, praktisch völlig uninteressante Unterschiede zu Signifikanzen führen. Jeder statistische Test
wird bei so großen Stichprobenumfängen zu einem "scharfen Schwert", dessen Handhabung Vorsicht und Training erfordert. Die Gefahr dabei ist, daß bei der Interpretation solcher Signifikanzen, die auf solch winzigen Effekten beruhen, eben diese praktisch uninteressanten Effekte übersehen werden und Interpreten sich voreilig zu spektakulären Interpretationen verleiten lassen - etwa zu astrologischen.

Erzeugung von Zusammenhängen

Nachfolgend wird anhand sehr einfacher Demonstrationsbeispiele mit mathematischer Strenge gezeigt, daß ein statistischer Zusammenhang auch dadurch zustande kommen kann, daß man zwei Populationen, in denen der betreffende Zusammenhang jeweils nicht besteht - z. B. zwei Populationen aus unterschiedlichen Jahrgängen - zu einer Population zusammenfaßt. Der bequemen Überprüfbarkeit zuliebe (ohne Computer!) wird für die Umfänge der beiden erforderlichen Populationen jeweils die Zahl 100 gewählt, was die Allgemeingültigkeit der zu beweisenden Aussage nicht beschränkt.

Population I: Unter 100 Personen befinden sich 8 mit dem Sternzeichen A, 50 besitzen eine Eigenschaft E (z. B. Todesursache gehört zu einer bestimmten Gruppe von Todesursachen) und 4 Personen mit dem Sternzeichen A besitzen E.

In dieser Population I sind A und E statistisch unabhängig, was man in sehr anschaulicher (aber mathematisch korrekter) Form so sieht: Die Wahrscheinlichkeit für E hängt nicht davon ab, ob eine Person zu Sternzeichen A gehört oder nicht; der Anteil von E unter den Personen mit A beträgt nämlich 4 von 8 also 50 % und der Anteil von E unter den Personen mit Nicht-A beträgt 50-4=46 von 100-8=92, also auch 50 %.

Population II: Unter 100 Personen befinden sich 10 mit Sternzeichen A, 40 mit der Eigenschaft E und 4 mit dem Sternzeichen A besitzen E. Die statistische Unabhängigkeit von A und E sieht man wieder so: Der Anteil von E unter den Personen mit A beträgt 4 von 10, also 40 %. Der Anteil von E unter den Personen mit Nicht-A beträgt 40-4=36 von 100-10=90, also auch 40 %.

Zusammengelegte Population I + II: Unter 200 Personen befinden sich 18 mit Sternzeichen A, 90 mit der Eigenschaft E und 8 mit dem Sternzeichen A besitzen E. In dieser Population sind A und E nicht statistisch unabhängig! Denn der Anteil von E unter den Personen mit Sternzeichen A beträgt 8 von 18, also 44,4 %, während der Anteil von E unter den Personen mit Nicht-A 90-8=82 von 200-18=182, also 45,1 % beträgt.

Deutet man die drei Populationen als Zufallsstichproben, so ergibt sich für den Chi-Quadrat-Unabhängigkeitstest (in einer jeweiligen 4-Felder-Tafel) für die Stichprobenergebnisse I und II der Wert der Testgröße beidemal zu Null und für die zusammengelegte Stichprobe zu 0,00247. Multipliziert man sämtliche Anzahlen in diesen drei Stichproben jeweils mit einem Faktor, so multiplizieren sich auch die drei Testgrößen-Werte mit diesem Faktor, d. h. es ist nur eine Frage, von welchem Stichprobenumfang an der durch Zusammenlegen sozusagen künstlich erzeugte statistische Zusammenhang auch als signifikanter Zusammenhang erscheint.

Angewendet auf den von Sachs untersuchten Zusammenhang zwischen Sternzeichen und Suizid bedeutet das: Legt man die Daten aus zwei verschiedenen Jahrgangsgruppen oder auch aus zwei Regionen (z. B. städtische Bereiche und ländliche Bereiche) zusammen, so kann dann solch ein "künstlicher" Zusammenhang entstehen, wenn - wie in den vorliegenden Demonstrationsbeispielen - sich in den beiden jeweiligen Populationen sowohl die Verteilung der Sternzeichen etwas unterscheidet, als auch der Anteil der Suizide verschieden ist. Daß zeitliche Änderungen der Sternzeichenverteilung tatsächlich vorkommen, wurde vorangehend anhand von Daten, die Sachs selbst verwendet, empirisch nachgewiesen. Für die Suizid-Anteile gelten zeitliche Änderungen als allgemein bekannt - ebenso wie Unterschiede zwischen Regionen. Im Hinblick auf zeitliche Änderungen der Suizidanteile sagt Sachs selbst (S. 157): "Zu manchen Zeiten wurde der Suizid gar Mode". Diese Demonstrationsbeispiele betreffen prinzipiell sämtliche der Sachsschen Untersuchungen von Zusammenhängen, z. B. auch den zwischen den Sternzeichen der Partner bei Eheschließungen. Dazu braucht man nur Sternzeichen A in den Populationen I und II von Ehepaaren als Sternzeichen des Mannes und die Eigenschaft E als Sternzeichen der Frau zu deuten.

Diese Hinweise bedeuten naturgemäß nicht, daß die von Sachs gefundenen - bzw. nach Eliminierung von methodischen Fehlern verbleibenden - signifikanten Zusammenhänge als falsch erkannt wären - sie stellen sie nur in Frage und erfordern Nachuntersuchungen, bei denen beispielsweise nur Daten von Personen mit gleichen Geburtsjahren für Unabhängigkeitstests ausgewertet werden.

Wie bereits im Kapitel "Sternzeichen und Suizid" gezeigt, sind weitere Untersuchungen auf der Basis neuer Daten noch zwingender erforderlich im Hinblick auf das sogenannte "multiple Testproblem".

Ein Ausblick - Oder: Die List der Vernunft?

Vielleicht überrascht es, wenn ich trotz der vorgebrachten Kritik an der "Akte Astrologie" die Meinung vertrete, daß Sachs auch ein großes Verdienst zukommt, das Verdienst nämlich, in einer breiten Öffentlichkeit die Einsicht verbreitet zu haben, daß astrologische Hypothesen, ebenso wie andere wissenschaftliche Aussagen empirisch überprüfbar sind - mit den Methoden der Mathematischen Statistik als Hilfmitteln. Dies wird bekanntlich von vielen Verfechtern anderweitiger esoterischer oder okkulter Hypothesen von vornherein bestritten - sozusagen in einer Art von Vorne-Verteidigung gegenüber empirischen Überprüfungen sowie der Mathematischen Statistik. Allerdings wurde vorangehend auch gezeigt, daß sich bei der Anwendung der erforderlichen statistischen Verfahren methodische Fehler einschleichen können, die die Ergebnisse in Frage stellen. Es wurde aber auch skizziert, wie man im Rahmen kritischer Nachuntersuchungen der bisher ausgewerteten Daten sowie von Untersuchungen anhand neuer Daten diese methodischen Einwände prinzipiell entkräften könnte. Groß wäre es, wenn Sachs selbst mit den ihm zur Verfügung stehenden Möglichkeiten seine Arbeit im Hinblick auf eine "Akte II" fortsetzte. Erst danach eventuell noch verbleibende, schwer erklärbare signifikante statistische Zusammenhänge zwischen Sternzeichen und menschlichem Verhalten würden echte interpretatorische Knacknüsse für Astro-Skeptiker darstellen. Der Weg von der bisherigen "Akte" zu einer solchen "Akte II" wäre dann wohl ein glanzvoller Beleg für Hegels Idee von der List der Vernunft, die gelegentlich auf kleinen Umwegen den Fortgang der Vernunft befördert.

 

Fußnoten

(1) Wie auch Sachs verwende ich hier den populären Begriff "Sternzeichen", obwohl mir - wie sicherlich auch Sachs - natürlich bekannt ist, daß aus astronomischer wie astrologischer Sicht eigentlich der Begriff "Tierkreiszeichen" der angemessene wäre.

(2)Alle in diesem Artikel angegebenen numerischen Ergebnisse habe ich mittels Taschenrechner gerechnet, soweit sie Tests zu einzelnen Sternzeichen betreffen. Diese Ergebnisse und viele weitere zeit- und rechenaufwendige Tests hat Herr Diplom-Kaufmann Dietmar Bremm - einer meiner ehemaligen Statistik-Studenten - aus verbliebenem Interesse an der Statistik auf seinem PC nachgerechnet bzw. neu durchgeführt und zwar insoweit unabhängig von mir, als wir lediglich in telefonischem und postalischem Kontakt standen. Herzlichen Dank dafür!

(3)Alle Seitenangaben in diesem Beitrag beziehen sich auf die 2. Auflage der "Akte Astrologie".

Die nachfolgende Klausuraufgabe stellte ich bei der Statistik-Zwischenprüfung für Wirtschaftswissenschaftler am 28. 2. 1998 an der Universität Würzburg. Sie war als eine von drei Aufgaben von 237 Kandidaten in einer vierstündigen Klausur zu bearbeiten:

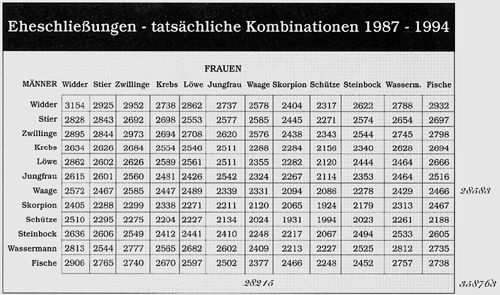
Nachstehend ist eine 12x12-Felder-Tafel aus "Gunter Sachs: Die Akte Astrologie - Wissenschaftlicher Nachweis eines Zusammenhangs zwischen den Sternzeichen und dem menschlichen Verhalten" als Kopie wiedergegeben - ergänzt durch drei handschriftlich vom Autor der Klausuraufgabe eingetragene Randwerte (=Randsummen), die die erforderlichen numerischen Rechnungen erleichtern.

In dieser Tafel sind die n= 358 763 Eheschließungen in der Schweiz im Zeitraum 1987 bis 1994 zweifach klassifiziert eingetragen und zwar einerseits bezüglich der 12-klassigen Einteilung "Tierkreiszeichen des Ehemanns" (12 Zeilen) und andererseits bezüglich der 12-klassigen Einteilung "Tierkreiszeichen der Ehefrau" (12 Spalten). Sachs teilt dazu mit, daß die Anwendung des Chi-Quadrat-Tests auf Unabhängigkeit auf diese 144-Felder-Tafel eine hoch signifikante Abweichung von der Unabhängigkeitshypothese ergibt und führt sodann für jedes der 144 Felder der Tafel einen Unabhängigkeitstest durch.

(a) Man überprüfe für das Feld "Waage x Waage" die Angabe von Sachs, daß bezüglich dieser Kombination die Unabhängigkeitshypothese bei Zugrundelegung einer Irrtumswahrscheinlichkeit von a = 0,05 abgelehnt werden kann, d. h. man teste bei Zugrundelegung einer Sicherheitswahrscheinlichkeit von 95 % mit Hilfe des Chi-Quadrat-Tests die Nullhypothese der Unabhängigkeit der Klasseneinteilungen {Waage-Ehemann; Nicht-Waage-Ehemann} und {Waage-Ehefrau; Nicht-Waage-Ehefrau}.

Die erforderliche 4-Felder-Tafel muß voll- ständig ausgefüllt angegeben werden. Ferner berechne man approximativ diejenige Irrtumswahrscheinlichkeit, die man zu akzeptieren hätte, falls man die Unabhängigkeitshypothese aufgrund des vorgelegten Stichprobenmaterials ablehnte. (Lösungshinweis: Die approximantive Nullverteilung der Testgröße ist die Verteilung des Quadrats einer nach N(0;1) verteilten zufälligen Variablen.)

Im Hinblick auf eine anschauliche Interpretation eines (eventuellen) signifikanten Ergebnisses berechne man vorsorglich Schätzwerte für folgende bedingte Wahrscheinlichkeiten: W (Waage-Frau | Waage-Mann), W (Waage-Frau | Nicht-Waage-Mann). Hierbei sehe man von der Problematik ab, daß es gemäß der Versuchsplanungsregel nach Durchsicht der 144 Kombinationen lediglich statthaft ist, Vermutungen über spezielle Zusammenhänge zu äußern und nicht statthaft ist, Signifikanzaussagen zu machen.

(b) Der in (a) durchzuführende Chi-Quadrat-Test "vergleicht" bekanntlich die tatsächliche Besetzungszahl 2331 des Feldes "Waage x Waage" mit dem (geschätzten) Erwartungswert für diese Besetzungszahl, wobei bei der Berechnung (bzw. beim Schätzen) dieses Erwartungswertes die Unabhängigkeitshypothese unterstellt wird. Im Hinblick auf eine mögliche Interpretation einer eventuell nachgewiesenen signifikanten Abweichung von der Unabhängigkeitshypothese, soll jetzt dieser Erwartungswert unter Zugrundelegung des folgenden Erklärungsmodells berechnet werden, wofür man vorübergehend die untersuchten Ehepaare als eine Grundgesamtheit von N= 358 763 Ehepaaren betrachte, in der es M1= 28 583 Waage-Männer und M2= 28 215 Waage-Frauen gibt. Erklärungsmodell: Nur 96,0 % der N Ehepaare, also 344 412 Ehepaare, wurden unter der Unabhängigkeitshypothese gebildet, d. h. nur für diese Paare beträgt die Wahrscheinlichkeit für die Kombination "Waage x Waage" M1/N . M2/N = 0,006266. Für die übrigen 4,0 % Ehepaare, also 14 351 Paare, sei die Wahrscheinlichkeit für "Waage x Waage" doppelt so groß wie bei Unabhängigkeit - weil bei der Paarbildung diese Kombination aus astrologischen Motiven von den Partnern als günstig angesehen wurde. Man berechne unter Zugrundelegung dieses Erklärungsmodells die totale Wahrscheinlichkeit dafür, daß ein zufällig herausgegriffenes Ehepaar zu "Waage x Waage" gehört. Mit dieser Wahrscheinlichkeit berechne man den Erwartungswert der Besetzungszahl für "Waage x Waage" für die obige Stichprobe von n= 358 763 Ehepaaren (auf eine Nachkommastelle genau).

(c) Man ersetze in der eingangs angegebenen 144-Felder-Tafel die tatsächliche Besetzungszahl 2331 für "Waage x Waage" durch die in (b) berechnete und ganzzahlig gerundete erwartete Besetzungszahl und führe den Unabhängigkeitstest aus (a) in der abgeänderten 4-Felder-Tafel durch, wobei man davon ausgehe, daß trotz dieser Änderung der tatsächlichen Besetzungszahl die Randwerte unverändert bleiben.

Lösungen:

Zu (a) erhält man - im Gegensatz zur Angabe von Sachs: Die formulierte Unabhängigkeits-Hypothese kann bei Zugrundelegung einer Sicherheitswahrscheinlichkeit von 95 % nicht abgelehnt werden. (Der Wert der Testgröße ergibt sich zu 3,62 und die zugehörige 95%-Testschranke hat den Wert 3,84.)

Zu (b) erhält man aufgrund des Erklärungsmodells für die Kombination "Waage x Waage" den Erwartungswert der Besetzungszahl zu 358763 . 0,006266 . 0,96 + 358763 . 2 . 0,006266 . 0,04 = 2337,9.

Führt man den Test aus (a) anstatt mit der tatsächlichen Besetzungszahl 2331 mit dieser erwarteten Besetzungszahl 2338 durch, so kann die Unabhängigkeits-Hypothese bei der Sicherheitswahrscheinlichkeit 95 % abgelehnt werden. (Für die Testgröße ergibt sich jetzt der Wert 4,26, der die bereits angegebene Testschranke überschreitet.) Anmerkung: Nach der zwischenzeitlich erfolgten Korrektur der Zwischenprüfung kann ich mitteilen, daß diese Aufgabe von den Teilnehmern offensichtlich als besonders leicht empfunden wurde. Teil (a) haben fast alle Kandidaten erfolgreich bearbeitet - auch die letztlich Durchgefallenen.

 

Dr. Herbert Basler ist Akademischer Direktor am Institut für Angewandte Mathematik und Statistik der Universität Würzburg. Er gilt als renommierter Statistiker. Sein Lehrbuch "Grundbegriffe der Wahrscheinlichkeitsrechnung und Statistischen Methodenlehre" ist bereits in der 11. Auflage erschienen. Eines seiner Spezialgebiete ist die stochastische Analyse des Lottospiels. Seine daraus entwickelten gewinnsteigernden Tippstrategien beim Lottospiel" basieren auf einer Analyse von 1264 Lotto-Ausspielungen im Zeitraum 1955 bis 1979 und konnten im nach hinein empirisch bestätigt werden.

 

Dieser Artikel erschien im "Skeptiker", Ausgabe 3/1998.